Почему нельзя делить на ноль — простое объяснение и последствия

Деление на ноль – это одна из самых фундаментальных и важных математических операций, с которой сталкивается каждый, изучающий математику, еще в школьные годы. Но что делает это действие таким особенным и почему оно запрещено?

Деление на ноль не имеет определения в математике, поскольку противоречит основным математическим законам и приводит к противоречивым и абсурдным результатам. Один из примеров — это «бесконечность», которая возникает, когда число делится на ноль. Но что означает «бесконечность» и почему она неприемлема в математике?

Бесконечность – это абстрактный математический объект, который обозначает бесконечно большое число, но не является числом само по себе. Она не подчиняется основным математическим правилам и аксиомам и, следовательно, не может быть использована в обычных действиях над числами. Попытка деления на ноль ведет к неопределенности и неприемлемым результатам, что делает это действие недопустимым в математике и других науках.

Почему деление на ноль невозможно?

Представим, что мы пытаемся разделить число a на ноль, то есть выполняем операцию a/0. Мы должны найти число x, которое удовлетворяет условию 0 * x = a. Однако, не существует такого значения x, которое при умножении на ноль даст нам определенное число a, так как любое число умноженное на ноль будет равно нулю. Таким образом, деление на ноль не имеет математического значения и не определяет результат.

В результате деления на ноль получается неопределенность. Это означает, что не существует одного единственного ответа на операцию деления на ноль, и результат может быть любым. В разных математических контекстах может использоваться специальное обозначение для обозначения этой неопределенности, такое как символ «∞» (бесконечность) в теории множеств или «NaN» (Not a Number) в компьютерной науке.

Последствия деления на ноль также могут быть непредсказуемыми. Например, в математических выражениях или алгоритмах, содержащих деление на ноль, это может привести к ошибкам или некорректным результатам. Поэтому, в математике и программировании важно избегать деления на ноль и проверять входные данные на эту возможность перед выполнением операции.

Определение деления на ноль

Многие математические операции имеют определенные правила, которые позволяют выполнять их без проблем. Например, сложение, вычитание и умножение определены для всех чисел и их результат всегда будет определен. Но деление на ноль является исключением.

Деление на ноль можно представить как попытку разделить что-то на ничто. Это противоречит основным математическим принципам и логике. Потому что при делении на ноль не существует определенного результата или значение. Это можно увидеть из примеров:

• 10 / 0 = ошибкa
• 0 / 0 = ошибкa

В обоих случаях деление на ноль приводит к ошибке, так как невозможно разделить число на ноль.

Поэтому деление на ноль запрещено и считается математическим нарушением. Оно приводит к неопределенности и возможным ошибкам в дальнейших вычислениях. При программировании или использовании математических формул, важно быть внимательным и избегать подобных делений, чтобы избежать ошибок и получить корректные результаты.

Что такое деление на ноль?

При делении на ноль возникает неопределенность, так как невозможно определить, какое число нужно поделить на ноль, чтобы получить исходное число. Например, если мы хотим разделить число 6 на ноль, мы не можем найти число, умножение которого на ноль даст нам 6.

Из-за этой неопределенности, деление на ноль является математической ошибкой и противоречит основным принципам алгебры и арифметики. Попытка выполнить деление на ноль приводит к ошибке или искажению результатов расчетов.

В программировании деление на ноль может вызвать ошибку выполнения программы или привести к непредсказуемым результатам. Например, если программа пытается разделить число на ноль, она может зависнуть или выдать сообщение об ошибке. Поэтому в программировании принято проверять, не является ли делитель нулем перед выполнением операции деления.

Избегание деления на ноль помогает избежать ошибок и обеспечить корректность математических и программных вычислений.

Последствия деления на ноль

1. Результат деления на ноль неопределен. Когда мы делим число на ноль, невозможно получить однозначный и корректный ответ. Вместо этого мы получаем неопределенное значение.
2. Математические выражения с делением на ноль становятся несостоятельными. Если в выражении присутствует деление на ноль, то все остальные части выражения также теряют смысл, и оно становится некорректным.
3. При вычислении деления на ноль возникает ошибка. Компьютерные программы и калькуляторы не могут выполнить операцию деления на ноль и выдают ошибку. Это может привести к сбою программы или неправильным результатам вычислений в программах, которые предполагают, что деление на ноль невозможно.
4. Деление на ноль может привести к бесконечности. В некоторых случаях, при делении числа на ноль, результат может стремиться к бесконечности. Это особенно верно при делении отрицательного числа на ноль.
5. Ноль является особым числом. Ноль имеет специальное значение в математике и служит нейтральным элементом для операции умножения. Деление на ноль нарушает основные законы алгебры, такие как закон нуля для умножения.

Итак, деление на ноль является недопустимой операцией и может привести к серьезным последствиям. Поэтому всегда важно помнить о том, что это математическое действие не имеет корректного значения и следует избегать его выполнения.

Математические последствия

Делить на ноль невозможно по ряду математических причин и последствий. Рассмотрим некоторые из них:

1. Непределенность. Если мы попытаемся разделить любое число на ноль, получим непределенное значение, которое не поддается однозначному определению. Например, если разделить 6 на 0, мы не сможем точно сказать, какое число получится в результате этой операции. Такая непределенность создает неопределенную ситуацию в математике.
2. Нарушение алгебраических свойств. Деление на ноль приводит к нарушению многих алгебраических свойств чисел. Например, если разделить число на ноль, то результатом этой операции будет бесконечность. Но в математике нет такого числа, которое могло бы быть равно бесконечности. Таким образом, деление на ноль противоречит алгебраическим законам и приводит к некорректным математическим выражениям.
3. Распространение ошибок. Если при расчетах допустить деление на ноль, это может привести к серьезным ошибкам и неверным результатам. Деление на ноль является частой ошибкой, которая может возникнуть при решении математических задач или при работе с формулами. Поэтому важно всегда помнить о невозможности деления на ноль и быть внимательным при выполнении математических операций.

Таким образом, деление на ноль в математике имеет серьезные последствия, связанные с непределенностью, нарушением алгебраических законов и возможностью распространения ошибок. Это объясняет, почему подобная операция считается некорректной и невозможной в математике.

Практические примеры

Давайте рассмотрим несколько примеров, чтобы увидеть, почему деление на ноль невозможно и какие могут быть последствия.

Пример 1: Представьте, что у вас есть 6 яблок и вы хотите разделить их поровну между 0 людьми. Нет ни одного человека, кому можно было бы отдать по яблоку. Разделение на ноль приводит к ситуации, в которой невозможно распределить яблоки.

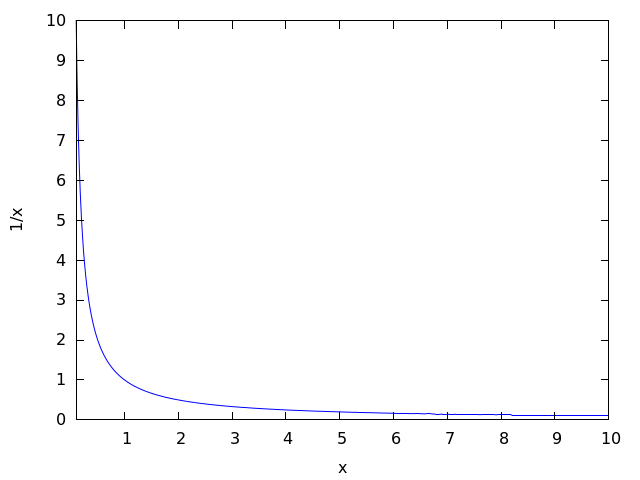
Пример 2: Рассмотрим простую формулу: 1 / 0. Если мы попытаемся вычислить эту формулу, то получим бесконечность. Однако, бесконечность — это не определенное число, а понятие, которое означает бесконечное увеличение, которое не может быть точно представлено в числовой форме.

Пример 3: В программировании деление на ноль может вызвать серьезные ошибки. Если мы позволим программе делить на ноль, она может зависнуть, выдавать неправильные результаты или даже вызывать сбои и прекращать работу. Поэтому при написании программ важно проверять исключительные ситуации и обрабатывать деление на ноль.

Итак, эти примеры показывают, что деление на ноль — это неопределенное действие, которое может привести к некорректным результатам и ошибкам. Поэтому в математике, физике, программировании и других областях следует избегать деления на ноль.

Избегайте деления на ноль

Почему деление на ноль запрещено? Понятие деления на ноль противоречит основным математическим правилам и логике. Деление обычно рассматривается как обратная операция умножению. Если мы знаем, что a * b = c, то мы можем найти c / b = a. Однако, когда b = 0, эта логика не работает: любое число, умноженное на ноль, равно нулю, то есть для любого числа a, a * 0 = 0. Но мы не можем определить, какое число нужно умножить на ноль, чтобы получить любое другое число.

Деление на ноль также приводит к математической неопределенности. Результатом деления на ноль может быть любое число, плюс или минус бесконечность, или даже неопределенное значение. Различные математические системы обрабатывают деление на ноль по-разному, но во всех случаях результат остается неопределенным.

Последствия деления на ноль не ограничиваются только математикой. Ошибка деления на ноль может привести к сбоям в программных системах и компьютерах. В программах и приложениях специальные проверки обычно применяются для предотвращения деления на ноль и соответствующих ошибок. Отсутствие этих проверок может привести к непредсказуемому поведению программного обеспечения.

Поэтому, важно помнить, что деление на ноль недопустимо в математике и программировании. При решении задач и написании программ всегда следует избегать подобных ситуаций и обрабатывать возможные ошибки деления на ноль.

Как предотвратить деление на ноль?

Чтобы предотвратить деление на ноль, необходимо проверять значения перед выполнением операции. Наиболее распространенным способом проверки является использование условных операторов.

Например, перед делением двух чисел можно проверить, что значение делителя не равно нулю:


if (делитель != 0) {
результат = делимое / делитель;
} else {
// обработка ошибки деления на ноль
}


Таким образом, мы проверяем, равно ли значение делителя нулю, и выполняем деление только в случае, если это не так. В противном случае, мы можем обработать ошибку или присвоить значение по умолчанию.

Предотвращение деления на ноль имеет большое значение в программировании. Если не учесть этого правила, код может вызывать ошибки, некорректно обрабатывать данные или приводить к непредсказуемым результатам.

Необходимо помнить, что ноль не может быть использован в качестве делителя. Будьте внимательны при написании кода и всегда проверяйте значения перед делением, чтобы избежать возможных проблем.

Вопрос-ответ:

Почему нельзя делить на ноль?

Деление на ноль в математике не имеет смысла и не определено. Деление представляет собой операцию, обратную умножению, и позволяет найти число, умножая другое число на обратное. Однако не существует такого числа, которое можно было бы умножить на ноль и получить конкретный результат.

Какими последствиями может быть деление на ноль?

Деление на ноль может привести к некорректным математическим операциям и ошибкам. Например, если разделить число на ноль, результатом будет бесконечность или неопределенность. Это может привести к непредсказуемым и нереалистичным результатам в расчетах и анализе данных.

Можно ли делить на ноль в компьютерных программах?

В большинстве программированных языков деление на ноль вызывает ошибку. Это сделано для защиты от некорректных вычислений и возможности контроля ошибок. В некоторых языках программирования, таких как Python и Java, деление на ноль может быть разрешено в определенных случаях, но результатом таких операций будет специальное значение, обозначающее бесконечность или неопределенность.

Есть ли исключения, когда можно делить на ноль?

В математике нет исключений для деления на ноль в обычной арифметике. Однако в некоторых областях математики, таких как теория пределов или теория множеств, можно рассмотреть предельные случаи, когда деление на ноль определено или имеет особое значение. Однако это является специальными случаями и не применимо в обычных расчетах и операциях.

Какая практическая польза от запрета на деление на ноль?

Запрет на деление на ноль помогает избежать некорректных вычислений, ошибок и нереалистичных результатов в математических расчетах. Кроме того, этот запрет является основой для определения и работы с другими математическими понятиями, такими как бесконечность, пределы, анализ функций и многих других.

Почему деление на ноль невозможно?

Деление на ноль невозможно, потому что математические операции имеют определенные правила и ограничения. В данном случае, деление на ноль противоречит этим правилам и не имеет смысла. Результат такой операции не определен и не может быть вычислен.